sudoku
How to build a brute force Sudoku solver
Follow my journey on how to build an algorithm that lets you create or solve Sudoku puzzles!
Follow my steps or jump ahead — this is the Jupyter notebook: https://gist.github.com/nickyreinert/966299333429ef685338e5feb5056126
Warmup — introduction
Before we start, we need to get familiar with how Sudoku works. I suggest we number each cell in the giant grid from 1 to 81. This way, we can programmatically loop from the top-left to the bottom-right to find valid solutions:
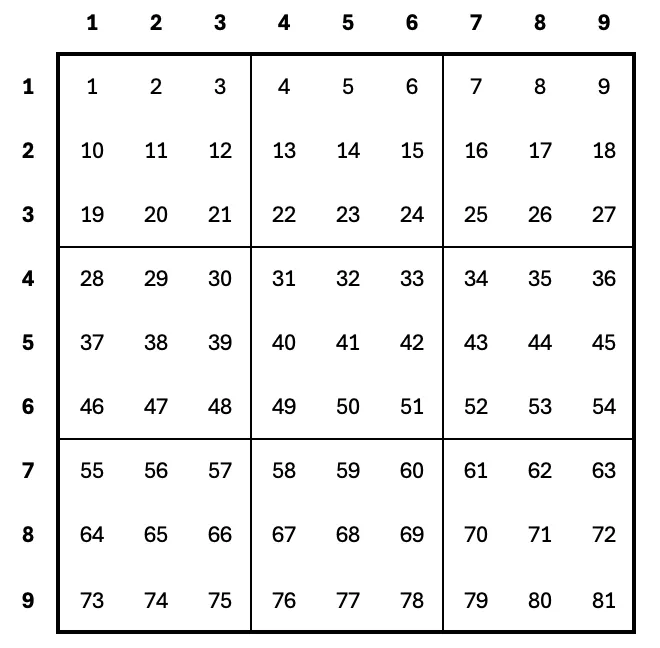
Sudoku has three rules: a number can’t exist twice in the same column, row, or section. So, first, we need a way to identify the column, row, and section for each position.
Every row contains 9 cells, so the row index is simply:
ceil(position / 9)
Or if you prefer double slash (//), which works like a “floor” function:
((position — 1) // 9) + 1
Columns probably also have something to do with 9 (because 9 is kind of a big deal in Sudoku). The first nine cells are exactly addressing their corresponding columns, obviously. So, in the upcoming rows (positions 10 and onward), we just need to reduce it back to 1 to 9. We can use modulo for that!
((position — 1) % 9) + 1
The section index is a little trickier. It’s a combo of the row and column index and some tweaks. There’s probably a clever mathematical approach, or you can just trial-and-error your way through (my usual strategy). Here’s a starting point:
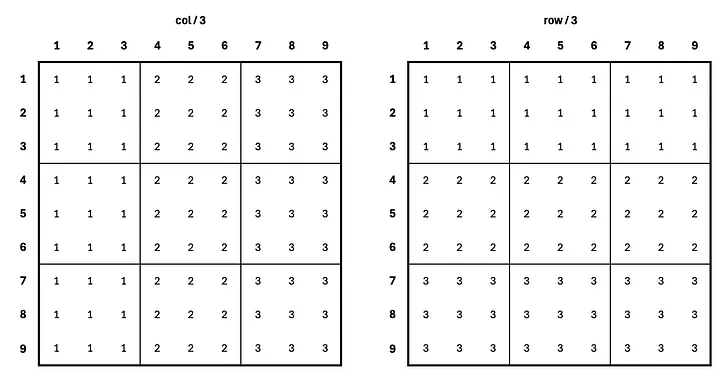
We take the floor of a third of each position now. It seems like we could just sum them to get the fitting section index, with a little adjustment. Here’s the magic:
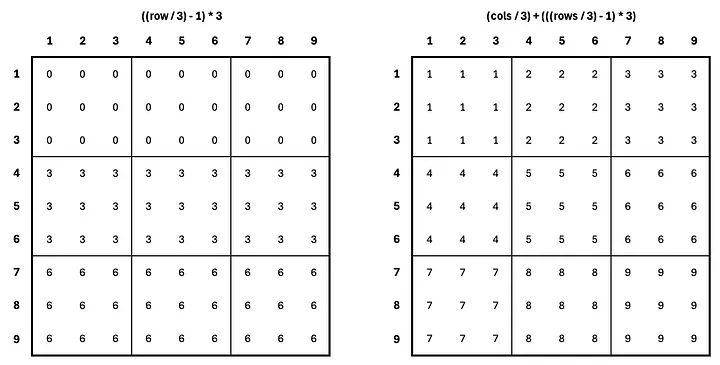
And that’s the formula to get the section index:
(col // 3) + (((row // 3) — 1) * 3)
First steps
Well, now that we know how to address each row, column, and section, let’s dive into the actual algorithm.
Solution approach
The basic idea is to iterate through the positions up to 81. At every step, we choose a number from 1 to 9 and check if it already exists in the corresponding row, column, or section (we’ll call these containers). If it does, the number is blocked for the current position, and we have to check the next number. If we can’t find a valid number for the current position, we need to roll back to the previous one and choose a different number. We repeat this process until we either reach position 81 — meaning we’ve found a valid Sudoku — or have to backtrack more.
Implementation in Python
We start by initializing four dictionaries to keep track of the numbers in each container. The solutions dictionary holds (surprise!) the valid numbers for the entire grid.
def reset_containers():
global rows, cols, sections, solutions
rows = {i: [] for i in range(1, 10)}
cols = {i: [] for i in range(1, 10)}
sections = {i: [] for i in range(1, 10)}
solutions = {}
reset_containers()
print(sections, '\n', rows, '\n', cols)
Result:
{1: [], 2: [], 3: [], 4: [], 5: [], 6: [], 7: [], 8: [], 9: []}
{1: [], 2: [], 3: [], 4: [], 5: [], 6: [], 7: [], 8: [], 9: []}
{1: [], 2: [], 3: [], 4: [], 5: [], 6: [], 7: [], 8: [], 9: []}
The visualize function takes the solution dictionary and returns a nice grid, displaying the numbers — you’ll find it in the notebook I referenced at the top!
def visualize(solution):
# see Jupyter notebook referenced on the top
We’ve already figured out how to get the actual row, column, or section from a given position. Now, let’s translate into Python and check if we’re on the right track:
print('pos', '\t', 'row', '\t', 'col', '\t', 'section')
for position in range(1, 82):
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
print(position, '\t', idx_row, '\t', idx_col, '\t', idx_section)
Output:
pos row col section
1 1 1 1
2 1 2 1
3 1 3 1
4 1 4 2
5 1 5 2
6 1 6 2
7 1 7 3
8 1 8 3
9 1 9 3
10 2 1 1
...
Yes, we are! Every position is correctly mapped to the correct container!
Solution checking and iterating
The first version is quite simple: We iterate through the positions and add a number that does not exist in one of the corresponding containers.
reset_containers()
number = 1
for position in range(1, 82):
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
if (number not in rows[idx_row] and number not in cols[idx_col] and number not in sections[idx_section]):
solutions[position] = number
rows[idx_row].append(number)
cols[idx_col].append(number)
sections[idx_section].append(number)
number += 1
visualize(solutions)
Seems like our basic loop is working fine. Let’s add some fine-tuning and limit it to the numbers from 1 to 9. We can just introduce an inner loop to keep things simple:
Output:
Seems like our basic loop is working fine. Let’s add some fine-tuning and limit it to the numbers from 1 to 9. We can just introduce an inner loop to keep things simple:
reset_containers()
number = 1
for position in range(1, 82):
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
for number in range(1, 10):
if (number not in rows[idx_row] and number not in cols[idx_col] and number not in sections[idx_section]):
solutions[position] = number
rows[idx_row].append(number)
cols[idx_col].append(number)
sections[idx_section].append(number)
break
visualize(solutions)
Output:
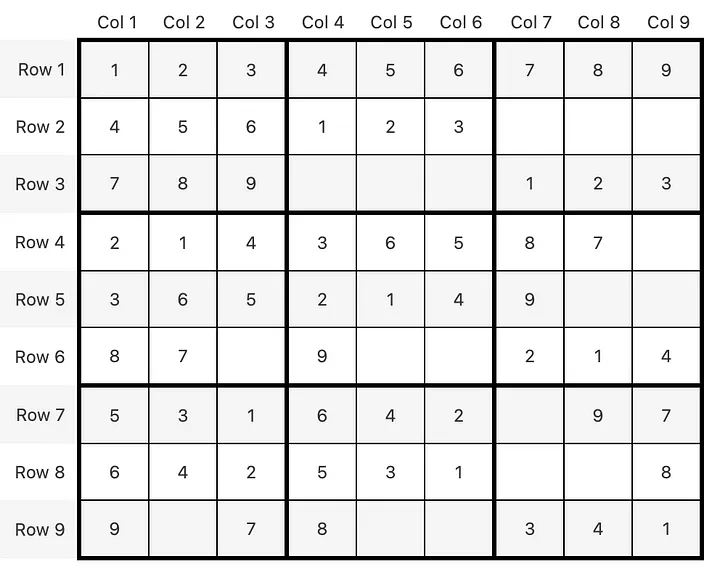
There are a lot of empty spots in the grid, what are we missing? Let’s introduce a conditional that stops when there’s no solution:
reset_containers()
number = 1
for position in range(1, 82):
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
for number in range(1, 10):
if (number not in rows[idx_row] and number not in cols[idx_col] and number not in sections[idx_section]):
solutions[position] = number
rows[idx_row].append(number)
cols[idx_col].append(number)
sections[idx_section].append(number)
break
if not position in solutions:
break
visualize(solutions)
Output:
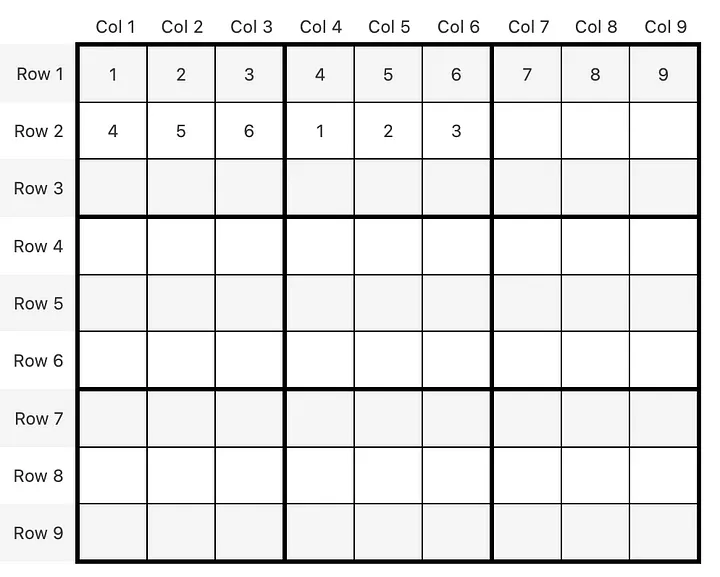
Quite good, but just stopping the loop when we hit a dead end probably won’t get us to a solution. We need to keep track of dead ends, and we need the ability to go back, choose another path, and try again. Let’s start with a container that holds “impossible” paths for each of our 81 positions.
We’ll also switch from a limited for-loop to an “infinite” while-loop because now we’re not just incrementing from 1 to 81 — we’ll be going back and forth. Of course, it’s always a good idea to use a stop condition, like max_iterations, so we don’t accidentally run into an actual endless loop when using while.
Let’s put all of that into a new “big” init function!
def reset_containers():
global rows, cols, sections, solutions, dead_ends
rows = {i: [] for i in range(1, 10)}
cols = {i: [] for i in range(1, 10)}
sections = {i: [] for i in range(1, 10)}
solutions = {}
dead_ends = {i: [] for i in range(1, 82)}
Now, if the current iteration doesn’t result in a solution, we don’t just stop processing. We go back one step:
position -= 1
And we archive the solution from the previous position as a “dead end solution”:
dead_ends[position].append(solutions[position])
Then we have to update our containers, as the solution is no longer valid:
rows[idx_row].remove(solutions[position])
cols[idx_col].remove(solutions[position])
sections[idx_section].remove(solutions[position])
del solutions[position]
Let’s see how this performs!
reset_containers()
print('iter', '\t', 'pos', '\t', 'row', '\t', 'col', '\t', 'section', '\t\t', 'number')
iteration = 1
position = 1
max_iterations = 10_000
stop = False
while True:
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
for number in range(1, 10):
print(iteration, '\t', position, '\t', idx_row, '\t', idx_col, '\t', idx_section, '\t\t', number)
iteration += 1
if (iteration > max_iterations): stop = True; break
if (number not in rows[idx_row] and \
number not in cols[idx_col] and \
number not in sections[idx_section] and \
number not in dead_ends[position]):
solutions[position] = number
rows[idx_row].append(number)
cols[idx_col].append(number)
sections[idx_section].append(number)
break
if stop: break
if not position in solutions:
position -= 1
if (position <= 0): stop = True; break
dead_ends[position].append(solutions[position])
print(f'rolling back {solutions[position]}')
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
rows[idx_row].remove(solutions[position])
cols[idx_col].remove(solutions[position])
sections[idx_section].remove(solutions[position])
del solutions[position]
else:
position += 1
if (position > 81): break
print(f'Done after {iteration - 1:,.0f} iterations.')
visualize(solutions)
Output:
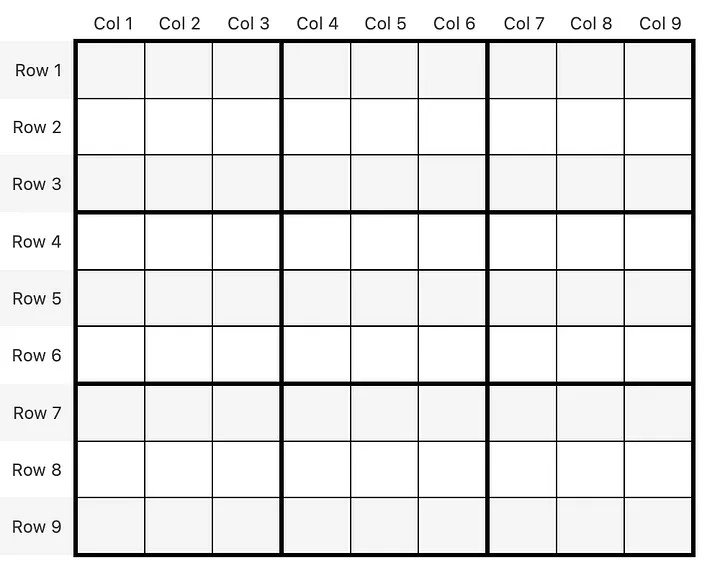
An empty grid? Why for flux sake? Well, our housekeeping is incomplete — we didn’t properly clean up the dead end container:
dead_ends[position] = []
Let’s take this chance to adjust our container reset function. It will now reset all containers or just the ones for a given position only:
def reset_containers(position = None):
global rows, cols, sections, solutions, dead_ends
if position is None:
rows = {i: [] for i in range(1, 10)}
cols = {i: [] for i in range(1, 10)}
sections = {i: [] for i in range(1, 10)}
solutions = {}
dead_ends = {i: [] for i in range(1, 82)}
else:
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
dead_ends[position].append(solutions[position])
rows[idx_row].remove(solutions[position])
cols[idx_col].remove(solutions[position])
sections[idx_section].remove(solutions[position])
del solutions[position]
And now the main loop:
def solve_game(max_iterations = 10_000):
global rows, cols, sections, solutions, dead_ends
reset_containers()
iteration = 1
position = 1
stop = False
# print('iter', '\t', 'pos', '\t', 'row', '\t', 'col', '\t', 'section', '\t\t', 'number')
while True:
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
for number in range(1, 10):
# print(iteration, '\t', position, '\t', idx_row, '\t', idx_col, '\t', idx_section, '\t\t', number)
iteration += 1
if (iteration > max_iterations): stop = True; break
if (number not in rows[idx_row] and \
number not in cols[idx_col] and \
number not in sections[idx_section] and \
number not in dead_ends[position]):
solutions[position] = number
rows[idx_row].append(number)
cols[idx_col].append(number)
sections[idx_section].append(number)
break
if stop: break
if not position in solutions:
dead_ends[position] = [] # if there were any dead ends on this position, remove them now, because we roll back
position -= 1
if (position <= 0): break
reset_containers(position) # and clean up containers for the previous position
else:
position += 1
if (position > 81): break
print(f'Done after {iteration - 1:,.0f} iterations.')
solve_game(max_iterations=10_000)
visualize(solutions)
Output:
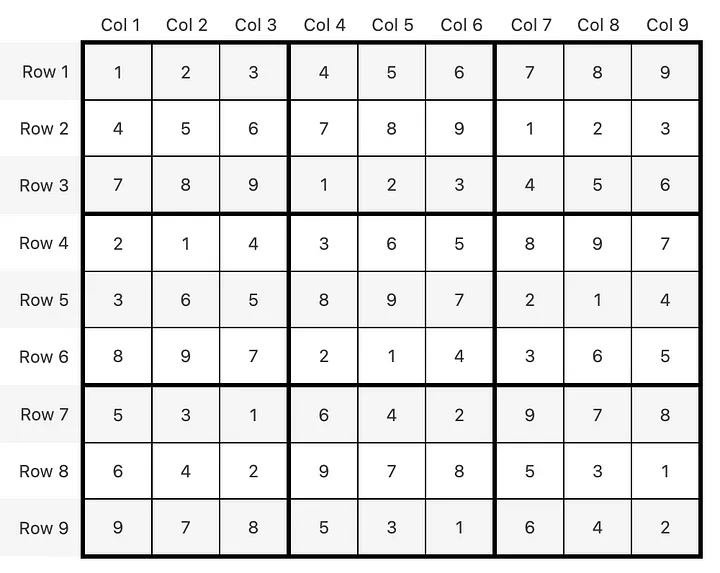
Wohaa! Looks like our little loop is already producing a valid result. But how does it perform when we add some numbers to the solution?
To work with a pre-filled grid, we need to implement another container — let’s call it target. We’ll add a simple check: If the target contains the current position, we’ll treat it as a constant. Copy it over to the other containers and skip to the next position:
if position in target:
number = grid[position]
rows[idx_row].append(number)
cols[idx_col].append(number)
sections[idx_section].append(number)
position += 1
continue
We also need to adapt the part where we move back one step when no solution can be found. If we move back from a regular position to a pre-filled one, we should instantly jump back to the last regular position. Otherwise, we’d get stuck in a loop. So, let’s declare last_regular_position, which points to the last regular cell before a pre-filled one, and handle the backtracking that way.
This should help avoid unnecessary loops and keep things running smoothly.
Our loop is growing:
def solve_game(debug = False, max_iterations = 10_000, target = {}):
global rows, cols, sections, solutions, dead_ends
reset_containers()
iteration = 1
position = 1
stop = False
start_of_occupied_area = 82
if debug: print('iter', '\t', 'pos', '\t', 'row', '\t', 'col', '\t', 'section', '\t\t', 'number')
# mandatroy: register all target position with our containers
for target_position in target:
idx_row = math.ceil(target_position / 9)
idx_col = ((target_position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
rows[idx_row].append(target[target_position])
cols[idx_col].append(target[target_position])
sections[idx_section].append(target[target_position])
while True:
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
if (position in target):
number = target[position]
solutions[position] = number
rows[idx_row].append(number)
cols[idx_col].append(number)
sections[idx_section].append(number)
if position < start_of_occupied_area: start_of_occupied_area = position
position +=1
continue
start_at = 1
if len(dead_ends[position]) > 0:
start_at = max(dead_ends[position]) + 1
for number in range(start_at, 10):
if debug: print(iteration, '\t', position, '\t', idx_row, '\t', idx_col, '\t', idx_section, '\t\t', number)
iteration += 1
if (iteration > max_iterations): stop = True; break
if (number not in rows[idx_row] and \
number not in cols[idx_col] and \
number not in sections[idx_section] and \
number not in dead_ends[position]):
solutions[position] = number
rows[idx_row].append(number)
cols[idx_col].append(number)
sections[idx_section].append(number)
break
if stop: break
if not position in solutions:
dead_ends[position] = []
if (position - 1) in target:
position = start_of_occupied_area - 1
else:
position -= 1
reset_containers(position)
else:
position += 1
if (position > 81): break
print(f'Done after {iteration - 1:,.0f} iterations.')
solve_game(debug = False, max_iterations = 5_000, target = {16: 2})
visualize(solutions)
Output:
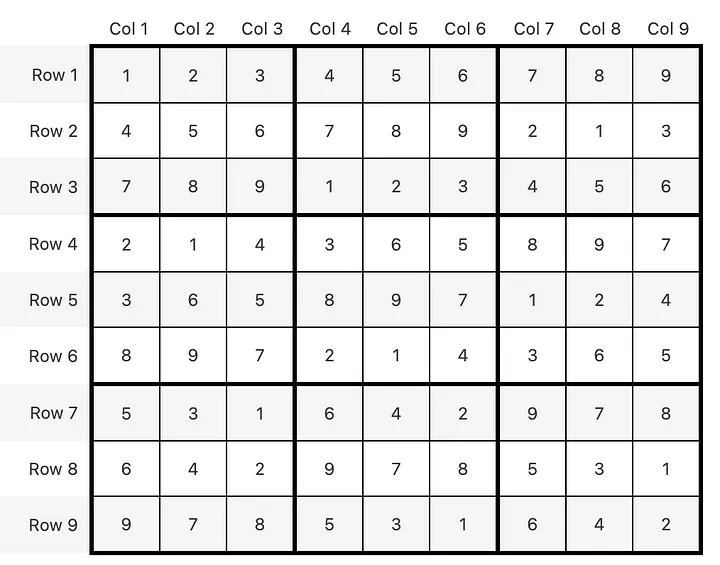
Farn-tastic! But don’t get too hyped, we’re not there yet. What about different solutions, variations? When we reach the last cell at position 81, in row 9 and column 9, we find exactly one solution for each previous cell. But how do we check for other options? To understand our next approach, imagine the solution as a huge 81-digit number, with all possible solutions branching out like a massive tree. The leftmost branch is the smallest number, and we’re going to find “higher” numbers, which are also valid solutions.
Let’s start with a simple idea: What if, as soon as we reach the end of the grid, we:
- Go back to the first item
- Store all numbers from the current solution to ignore them in the next iteration
- Switch to a new, empty solutions container
- And start over from the first position?
Well, I’ll spare us the effort of implementing it and instead ask you to think it over for yourself. You’ve got 5 milliseconds until the next paragraph starts…
Ka-ching! (Do you remember Lockerz from 2009? Why did I invest my time into that scam instead of Bitcoin? Whatever…)
It wouldn’t work! The first cell accepts 1 to 9 as possible options — our main branches of a tree. At the second level, which is the second cell, again we have 1 to 9 as possible values. Solution 1 already gave us this path:
1 - 2 - ...
But if we ruled out the 1 when iterating through the second solution, we’d also rule out another possible path:
1 - 3 - ...
So, instead of resetting to the first cell, the top of the tree, we just move back to the last cell — or the last node in the path or branch, however you want to call it. Right now, it looks like this:
... - 6 - 4 - 2
Think of the solution as a big number:
...642
From the previous run, we know that the following paths (or numbers) aren’t possible:
...611
...621
...631
...641
...642 - ka-ching!
Because, for some reason, the loop always took us back until we eventually hit the 4 and the 2. Now, what happens if we search for the next solution by going back to 81 again, but this time adding the 2 to our list of “dead ends”? The loop will run as it has before:
...643 - not possible, step back
...65 - not possible, step back
...7 - not possible, step back
It will keep doing that until — spoiler alert — it reaches position 66 (row 8, col 3):
...642
And it will try again, testing all possible numbers until it eventually hits:
...648
Which is the start of a new possible solution!
Sounds about right, doesn’t it?
Let’s implement it! First, a small adjustment to our init methods and our solutions container, which now holds multiple solutions:
solutions[solution_index][position]
Of course, we also need to adjust the function’s signature and how we reset our solution container. The way we address positions in the solution deck changes, too. It’s a list now, which makes it easier to slice the first n items of it (honestly, I don’t know why we didn’t do that from the beginning — it’s not really harder to handle. Guess that’s what they call “learning by doing” ;) ).
def reset_containers(solution_index, position = None):
global rows, cols, sections, solutions, dead_ends, burned_numbers
if position is None and solution_index == 1:
rows = {i: [] for i in range(1, 10)}
cols = {i: [] for i in range(1, 10)}
sections = {i: [] for i in range(1, 10)}
solutions[solution_index] = {}
dead_ends = {i: [] for i in range(1, 82)}
else:
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
if position in solutions[solution_index]:
number = solutions[solution_index][position]
del solutions[solution_index][position]
elif position in burned_numbers:
number = burned_numbers[position]
dead_ends[position].append(number)
rows[idx_row].remove(number)
cols[idx_col].remove(number)
sections[idx_section].remove(number)
Our solution method changes a little. Instead of stopping the loop when position > 81, we add the current solution to our “dead end” container and then go back to position 81.
def solve_game(debug = False, max_iterations = 10_000, target = {}):
global rows, cols, sections, solutions, dead_ends, burned_numbers
solution_index = 1
solutions = {solution_index: {}}
reset_containers(solution_index)
report_success = False
iteration = 1
position = 1
stop = False
burned_numbers = {} # keeps the previous solution
start_of_occupied_area = 82
if debug: print('solution', '\t', 'iter', '\t', 'pos', '\t', 'row', '\t', 'col', '\t', 'section', '\t\t', 'number')
for target_position in target:
idx_row = math.ceil(target_position / 9)
idx_col = ((target_position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
rows[idx_row].append(target[target_position])
cols[idx_col].append(target[target_position])
sections[idx_section].append(target[target_position])
while True:
if position <= 81:
idx_row = math.ceil(position / 9)
idx_col = ((position - 1) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
if (position in target):
solutions[solution_index][position] = target[position]
if position > 1 and position < start_of_occupied_area: start_of_occupied_area = position
position +=1;
continue
# if the current position has a burned number from the previous solution
# we can take this + 1 as the next starting point
# this should only happens once for each run when move backwards
start_at = 1
if position in burned_numbers:
last_found_number = burned_numbers[position]
start_at = last_found_number + 1
# note how we clean or contains only, not the actual burned_numbers record
# because if this iteration is not succesful, we need a reference!
del burned_numbers[position]
elif len(dead_ends[position]) > 0:
start_at = max(dead_ends[position]) + 1
for number in range(start_at, 10):
if debug: print(solution_index, '\t\t', iteration, '\t', position, '\t', idx_row, '\t', idx_col, '\t', idx_section, '\t\t', number)
iteration += 1
if iteration % (max_iterations // 10) == 0: report_success = True
if (iteration > max_iterations): stop = True; break
if (number not in rows[idx_row] and \
number not in cols[idx_col] and \
number not in sections[idx_section] and \
number not in dead_ends[position]):
solutions[solution_index][position] = number
rows[idx_row].append(number)
cols[idx_col].append(number)
sections[idx_section].append(number)
break
if stop: break
if not position in solutions[solution_index]:
dead_ends[position] = []
# this is also very important: when we are at this point
# we couldn't find a solution for the current position
# so we step back to the next "free" cell
# that is not blocked by a "target"
if (position - 1) in target:
position = start_of_occupied_area - 1
else:
position -= 1
# and then we clear the containers for this position, to have a fresh start
reset_containers(solution_index, position)
else:
position += 1
else:
idx_row = math.ceil((position - 1) / 9)
idx_col = ((position - 2) % 9) + 1
idx_section = math.ceil(idx_col/3) + ((math.ceil(idx_row/3) - 1) * 3)
# we found a complete solution, now record the numbers as "burned" for the next run
# for the next solution
if report_success == True: print(f'{solution_index} solutions completed after {iteration - 1:,.0f} iterations.'); report_success = False
# take over previous solutions as "burned numbers"
dead_ends = {i: [] for i in range(1, 82)}
# and also some house keeping, as
# we crawl back when trying additional solutions
# we only fill the part of the tree
# that actually changes, that's why we need to take over
# everything that did not change:
if solution_index >= 2:
solutions[solution_index] = {pos: solutions[solution_index][pos] if pos in solutions[solution_index] else solutions[solution_index - 1].get(pos) for pos in solutions[solution_index - 1]}
burned_numbers = solutions[solution_index].copy()
# it took me some time to find that out:
# basically we are telling the script to rewind
# as we do when we don't find a solution
# so we also need to remove the current number from our
# containers
number = solutions[solution_index][81]
rows[idx_row].remove(number)
cols[idx_col].remove(number)
sections[idx_section].remove(number)
position = 81
solution_index += 1
solutions[solution_index] = {}
print(f'Done after {iteration - 1:,.0f} iterationsm found at least {solution_index - 1} solutions')
solve_game(debug=False, max_iterations=1_000_000, target = {80: 7})
visualize(solutions[len(solutions) - 1])
And that’s our achievment:
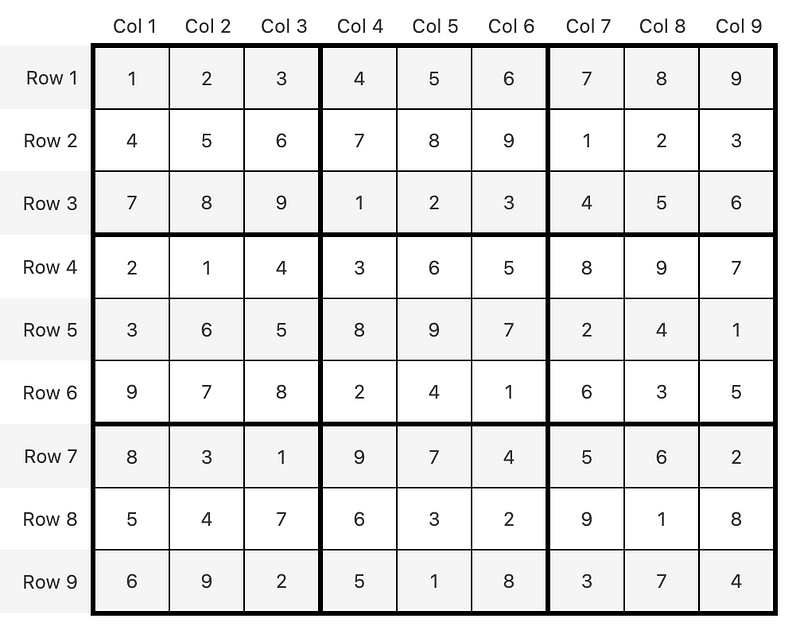
Our brute-force Sudoku solving algorithm is ready! Well, I bet there are a couple of steps to optimize — not only code-style-wise, but also to make it run faster. I’d say that’s your homework. There are 6,670,903,752,021,072,936,960 possible paths (that’s 6 sextillion and a bit more, it can be writte as ~6 x 10^21, which is a reference to Blade Runner: Dr. Ana Stelline was born on the 10/6/21). Can you catch them all? How long does it take on your machine to get 1 million solutions?

Just one more thing… I asked ChatGPT to build a small function that checks if all solutions are valid. Wait, what? ChatGPT? Why haven’t we asked it earlier?
Because developing algorithms is fun?
You got it! Whatever, here we go:
def check_sudoku(solutions):
print('All good!')
Just kidding — you’ll find the actual implementation in the notebook. Before I send you off into your well-deserved time off, let’s quickly go over some visualizations. I “discovered” 295,295 solutions (took me 100 million iterations and roughly 45 seconds), and this is how they look like in an image:
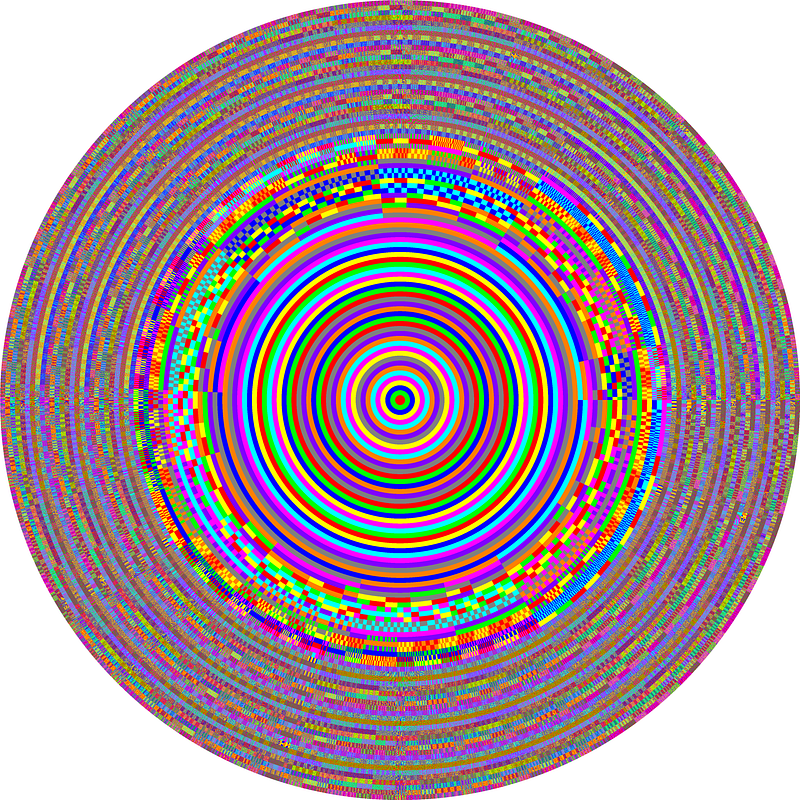
Finding 300,000 solutions out of 6 sextillion possibilities is like picking a single grain of sand from all the sand on Earth.
For the following visualization, I calculated the difference between each solution — remember, they’re all essentially enormous numbers!
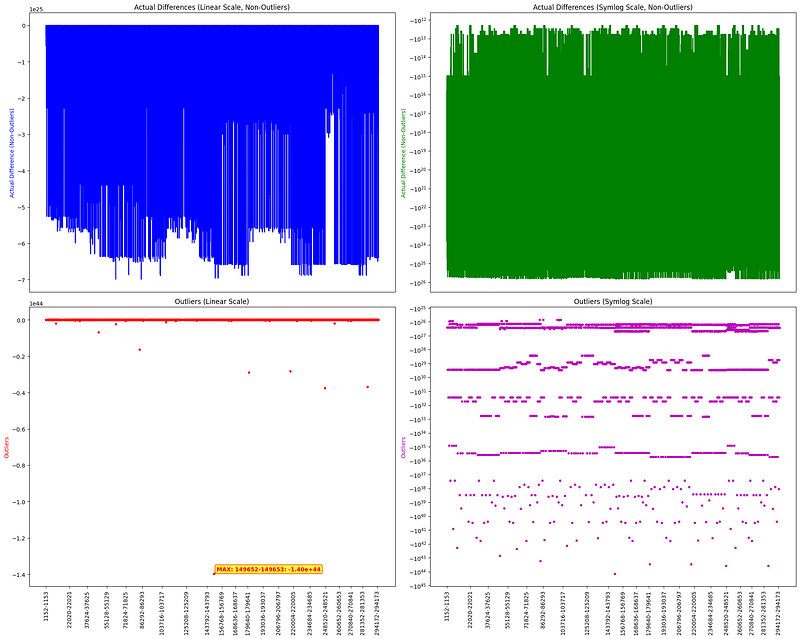
There are some interesting points to observe. On the symlog scale of outliers, you can clearly see bands of numbers. There’s also one outlier way out of the region, meaning that from solution 149,652 to 149,653, the loop has to revert to a very high position in our “solution tree.”
Can you find any more salient features? Let me know!