(or: How does blockchain mining work?)

A miner has to solve a mathematical problem to validate a block for the Blockhain. The so called Proof of Work requires a lot of computing power aka energy and therefore is quite expensive. Googles BigQuery has a price model, that charges you for the transferred data and not the computing power. Meaning: You can utilize a lot of computing power for free. If you are able to reproduce the mining algorithm in SQL.

In this article I first will explain how the mining process works. This is the main concept for a couple of Blockchain technologies. My explanation is based on Bitcoin’s blockchain. If you are already familiar with that, you may skip to part 2, where I present an SQL query that does the job.

Part 1: The mathematical problem aka: Mining a block

What’s a hash again?

A hash is a kind of unique piece of information calculated from any given input (I wrote about that earlier). There are a lot of hashing algorithms. The blockchain we are talking about uses SHA256. It’s important to understand, that a hash is basically just a really large number with always the same length: 256 bit.

If you change the input, even just a little, the hash changes. This makes the hash a pretty good indicator to check if the input data has been tampered: If you know the original hash and you re-calculate the hash for a given information, and both hashes are different, the initial information has been changed.

Why does the blockchain rely on hashes?

Every block in a blockchain contains two kind of information: A couple of transactions details and a block header. Among other details the header contains two important hashes: One hash for all the transactions of the current block and one hash for the header of the previous block.

If you would tamper the transaction data of lets say block #1337, the hash of this block’s header would change. But as the next block’s header contains a hash for the original block #1337, you could simply compare both hashes and come to the conclusion, that the data in block #1337 has changed.

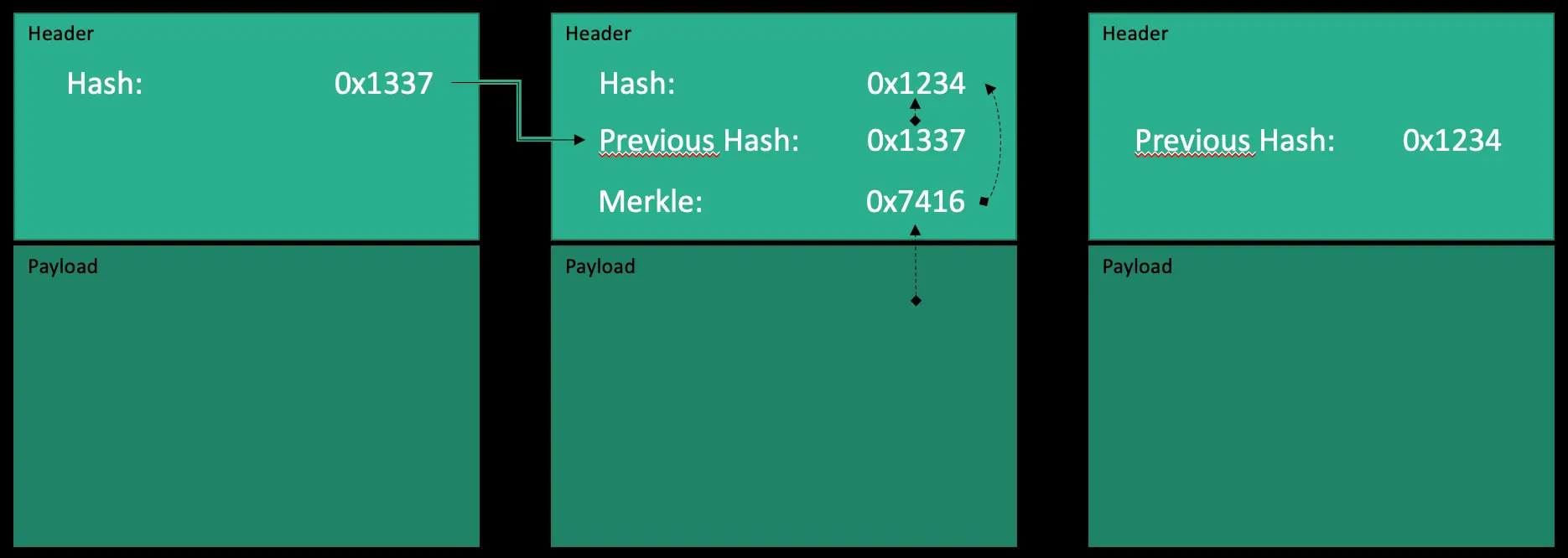
This sounds easy, because calculating one hash only takes milliseconds, even on slow computers. That’s why the blockchain protocol defines a very special requirement that every header’s hash has to meet: The hash of a block header has to be lower than a given number, the target.

S ide note: Besides that there are some other rules that make the calculation even more difficult: For example you need to double-hash the information and you need to calculate the Merkle root of all transactions of the current block.

You can meet this requirement by simply adding an incrementing number to the header information, re-calculate the hash, and see if the new hash is below the target.

The whole process is so complicated, that even powerful computers will take around 10 minutes to find a solution. That’s by the way a reason why Bitcoin is not the payment method: If you’d like to buy a coffee, you may have to wait around 10 minutes until your transaction is confirmed.

The block header

Let’s see what kind of information a block header contains. This is the header of block number 727938:

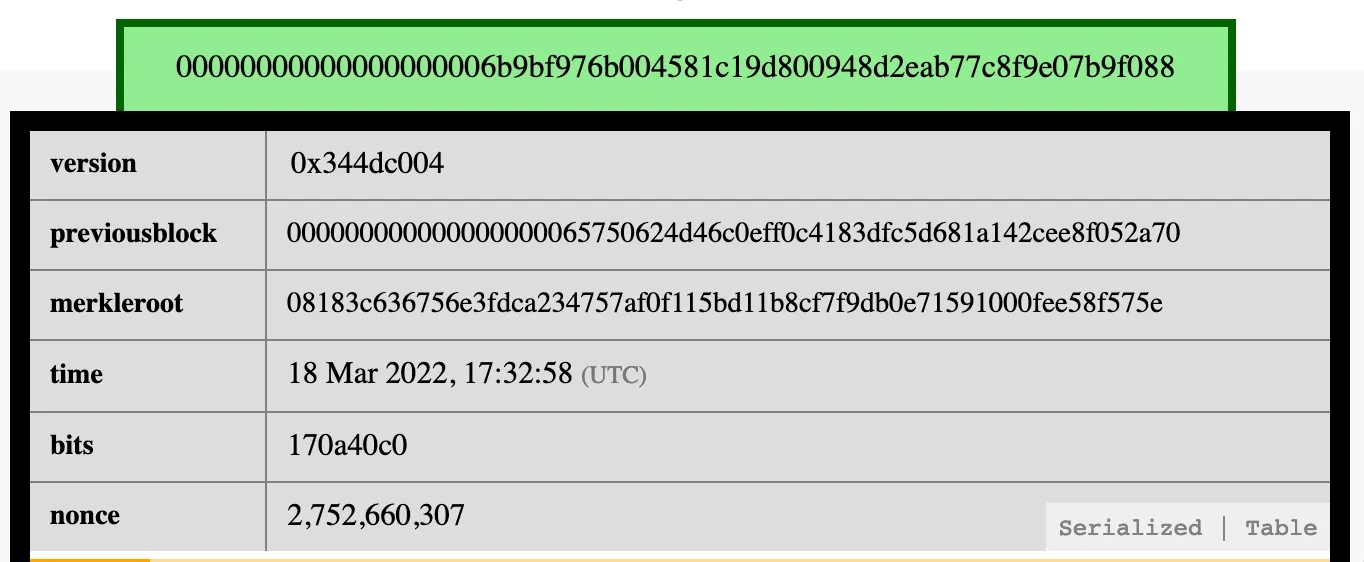
You will find six important fields here:

• a version field,
• the hash for the previous block’s header,
• the Merkle root,
• a timestamp,
• a bits field, that defines the target and
• a nonce

Let me describe those fields in detail:

The nonce field

If you take all header fields except the nonce field, you get the block message:

04c04d34702a058fee2c141a685dfc3d18c4f0efc0464d625057060000000000000000005e578fe5fe001059710edbf9f78c1bd15b110faf574723cafde35667633c18084ac23462c0400a17

The SHA256 hash for this looks like that:

5c96f247d3c6a48b244be859d888dd1ee2a80dd6378cc7e10f31b9d14b78660b

As mentioned above, the protocol requires you to add a specific kind of information to the block message, that leads to a hash below a given value. For starters lets make that easy: Find a number that leads to a hash starting with a zero. What if we add a 1 to the block message? (Remember: This is a hexadecimal number, so I need to add two digits):

04c04d34702a058fee2c141a685dfc3d18c4f0efc0464d625057060000000000000000005e578fe5fe001059710edbf9f78c1bd15b110faf574723cafde35667633c18084ac23462c0400a17**01**

That’s the resulting hash:

855ccd41ef49272ab633eff0cf5abed6d543ed5183eaf9f8a32e12a57b7419a9

No leading zeros? You may get a picture of how difficult it is. The actual target value for this block was a hash with 19 leading zeros. The miner need to (find and) add the number 1.396.904.612 (in hexadecimal 0x534312a4) to the block message to find a fitting hash. And that number is called **nonce **— short for number used once. That’s the resulting hash:

00000000000000000006b9bf976b004581c19d800948d2eab77c8f9e07b9f088

While calculation one hash seems pretty simple, imagine how long it would take for 1 Billion calculations, or even more? Even more? Yes, you heard right: The nonce is a four byte number meaning you have 2³² possible numbers (4,294,967,296) to check (the so called search space). And sometimes that’s not enough.

The previous block’s header hash

This is just the hash of the header of the previous block. Not much to say here: You cannot change it.

The bit field

This field defines the above mentioned target. It’s a 4 byte number, too:

0x170a40c0

A hash is a number with 32 bytes. And that’s strange: How can you limit a 32 byte number using only 4 bytes? Here it is: The first byte of the bit field defines an exponent: 0x17. The remaining 3 bytes define the mantissa: 0x0a40c0. The base is 256 and you need to substract 3 (length of the mantissa) from the exponent. So this is the formula to calculate the target:

target = 0x0a40c0 × 256⁽⁰ˣ¹⁷ ⁻ ³⁾⁾

The target will be adjusted every 2,016 blocks, which is roughly two weeks (6 blocks per hour × 24 hours × 7 days x 2 = 2,016). Why? The mathematical problem needs to be difficult enough to keep the chain safe but it must not be to difficult, because you do not want to wait more than 10 minutes for a transaction to be confirmed. As computing power changes or miners joining and leaving the network, the target and therefore the difficulty as to be adjusted.

The Merkle root

The Merkle root is a hash of all transactions of **the current block **(and a little more, I’m not going to much into detail here). Basically it’s pretty easy: You take two transactions and hash them to get Hash #1. Then you take two more transactions, hash them and get Hash #2. Now you take Hash #1 and Hash #2, hash it and get: Hash #3. You’re building an upside tree, where the transactions are on the bottom and the branches are dozens of hashes eventually leading to the root hash.

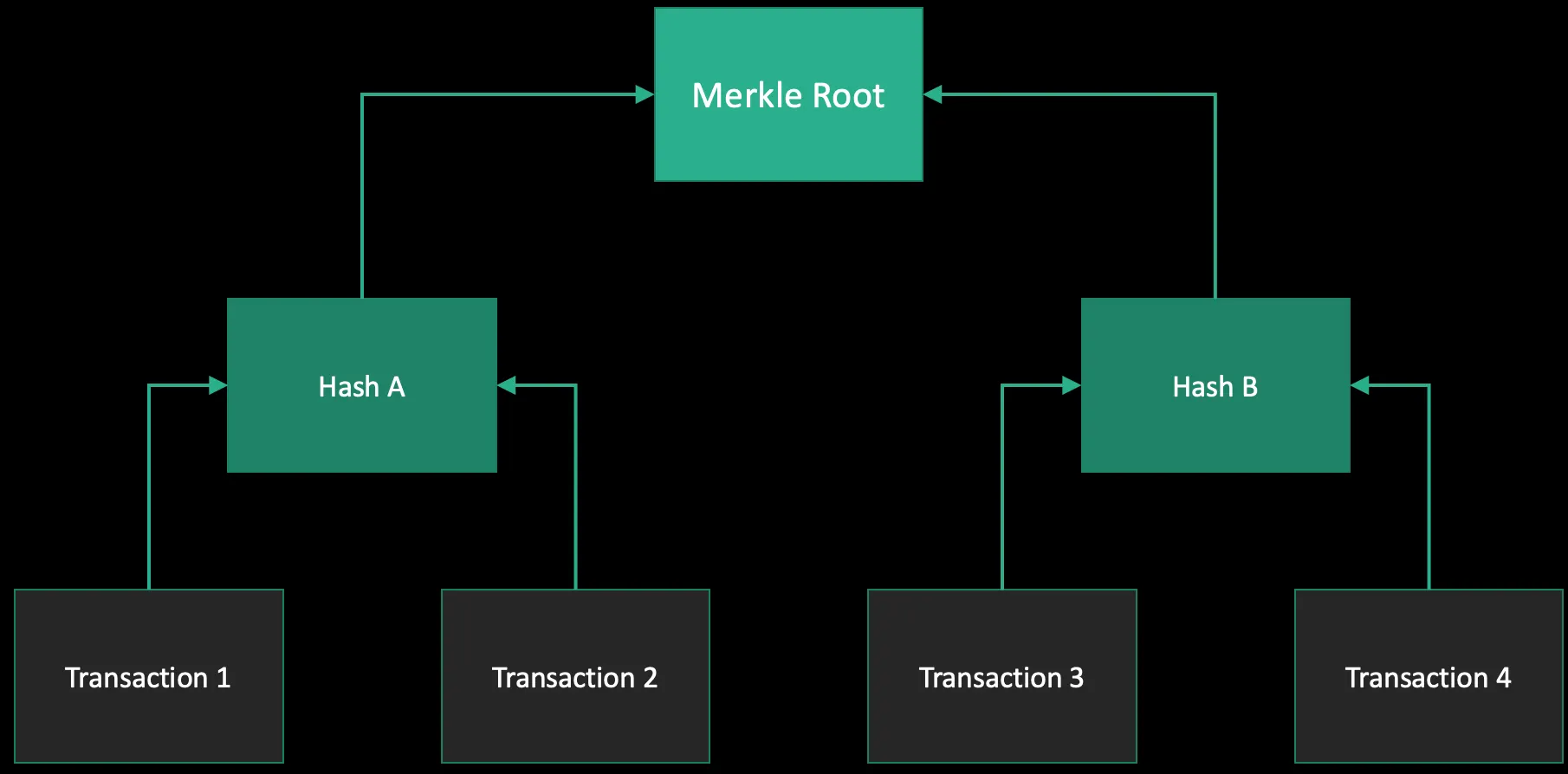
If the search space is not enough, the miner can change the order of the transactions to create a different Merkle root. This would change the block message and therefore lead to a different hash.

The timestamp

The timestamp, well, shows at what time the block was validated. In fact there is a lot more to tell about the timestamp, but not in a mathematical way.

The protocol uses the timestamp to see, how fast blocks are mined. As already explained, the network uses this value to adjust the difficulty.

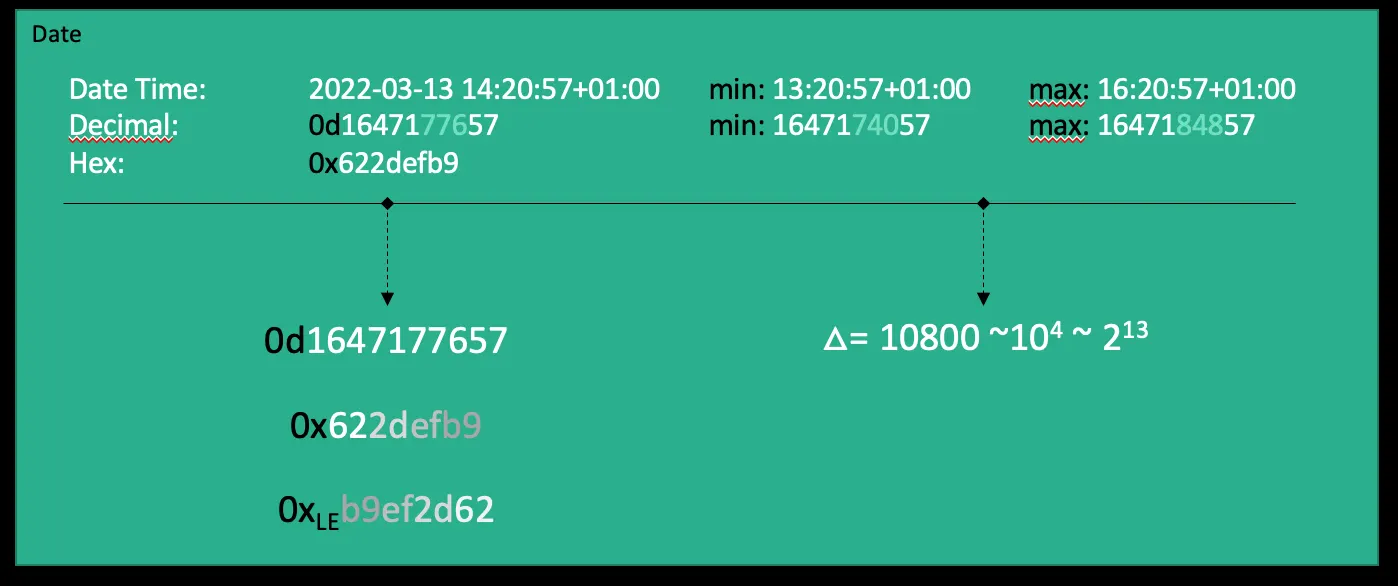
A miner can use the timestamp field to increase the search space. A valid timestamp has to be greater than the median timestamp of the last 11 blocks and lower than the network-time plus 2 hours. Eventually this gives you a 3 hour window where you can adjust the timestamp to gain extra search space. 3 hours are 10,800 seconds (which is roughly 2¹³).

The version field

Last but definitely not least: The version field contains a lot more than you would expect. The version field is 4 bytes long and it

• contains the current protocol version,
• signals readiness for soft fork proposals and
• offers additional search space.

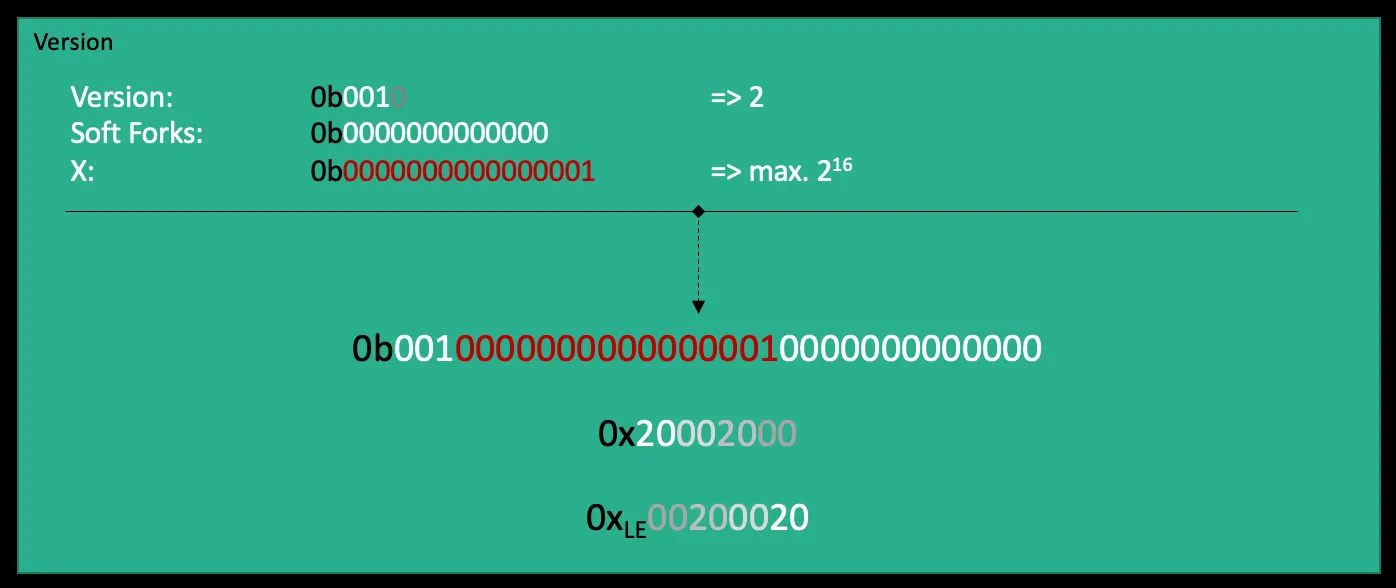
That’s a lot of information and it’s not that easy to pull it out of those 4 bytes. The current protocol version requires the **first 3 bits **(!) to be at least 0b001 (2 in decimal):

Besides that, the last 13 bits are used for soft forks signaling. This simply means, if a miner is ready for a particular soft fork, he flips on of those bits to 1. Imagine there’s a soft fork BIPx that requires the 1 bit to be flipped, that’s how the miner signals readiness for BIPx:

This would lead to a version field like this:

0x20000001

As you may have noticed, this leaves 16 bits open (32 bits at all, mins 3 bits for the version and 13 bits for soft forks = 16 bits left). This gives the miner 2¹⁶ more options to find a good hash! That technique is called overt ASIC boost. Lets take the version field from block #727938 for example: 0x344dc004

This is the bit representation of the hexadecimal value:

So apparently the miner took 0b1010001001101110 (0d41582) as an additional resource to finally find the fitting nonce 0xa4124353.

Block header summary

So after all you have six fields in your header, where only two fields are fixed and cannot be changed in order to find a hash below the given target: The bit field, that describes the target itself and the hash for the **previous header — **the vital element of the Blockchain concept..

Besides that you may change the nonce, the one field actually designed to change. The Merkle root, by re-arranging or considering different transactions. The version field and the timestamp by exploiting the 3 hour time window.

To give you an idea how complex it is to utilize at least the nonce and the version field, I created a Python script that does that for you:

Part 2: Using SQL and BigQuery to validate a block

Now as you are an expert in mining, let’s try to find a way to mine for free. I will implement a mining algorithm in SQL that iterates through the nonce and the additional version bits to find a hash below a required target. I’m not re-arranging the Merkle root and I will take the timestamp as a given value.

To make the whole process understandable, I will start from within the inner loop and calculate the hash from a given header, that already contains all the correct “answers”. I’m using the header for block #727155 with all the information already in the right format. After we understand the hashing process in BigQuery, we will build the header field by field and finally add the two loops.

And here they are — the variables for my six header fields. Remember that the version field contains the actual version as well as the soft fork signals.

# header for block 727155DECLARE hash_prev_block STRING DEFAULT "00000000000000000004136135b2e0cd367b56ea6c0dd5b8f79964a4cd7d2718";DECLARE merkle_root STRING DEFAULT "0d14fac91555d6337b10b2f20de231858fb5225f2ff685cd9b487c235d6e8307";DECLARE header_datetime STRING DEFAULT "622defb9";DECLARE bits STRING DEFAULT "170a3773";DECLARE nonce STRING DEFAULT "c8f05860";DECLARE version STRING DEFAULT "20002000";

We simply need to concatenate everything into one string before we hash it. Simply? Wait…there’s one pitfall called Little Endian. Bitcoin wants you to work with values in Little Endian. This is the way how you can write a number. In one sentence: Little Endian starts with the lowest value on the left. Basically you just switch the order of the single digits in your number. Instead of 23 you write 32. The value though remains the same. You achieve that using the REVERSE() function in SQL.

But beware — there’s more: What would you expect if you reverse the following hexadecimal value to Little Endian?

ABCDEF

Is it FEDCBA? No. We are working with bytes. One byte is 8 bits which is enough space for 255 values or in hexadecimal: FF. Two digits. That means we have to see all them values in pairs of two and the correct Little Endian representation is:

EFCDAB

To get this result you need to read the incoming value in bytes format and afterwards transfer it back to hexadecimal string. So this is how we create the actual header:

DECLARE header STRING;SET header =    TO_HEX(REVERSE(FROM_HEX(version))) ||    TO_HEX(REVERSE(FROM_HEX(hash_prev_block))) ||    TO_HEX(REVERSE(FROM_HEX(merkle_root))) ||    TO_HEX(REVERSE(FROM_HEX(header_datetime))) ||    TO_HEX(REVERSE(FROM_HEX(bits))) ||    TO_HEX(REVERSE(FROM_HEX(nonce)));

And that’s the header containing all relevant fields in Little Endian:

0020002018277dcda46499f7b8d50d6cea567b36cde0b23561130400000000000000000007836e5d237c489bcd85f62f5f22b58f8531e20df2b2107b33d65515c9fa140db9ef2d6273370a176058f0c8

The Hashing

BigQuerys build-it SHA256 expects a string or a byte but the header is made of hexadecimal values. So first we need to prepare the header, meaning: convert the hexadecimal string to the bytes format:

DECLARE b_header BYTES;SET b_header = FROM_HEX(header);

Now we can apply SHA256. And as mentioned above, we need to do it two times. The result of SHA256 comes in bytes, o we have to convert it back to a hexadecimal string:

SELECT TO_HEX(SHA256(SHA256(b_header)))

That finally leads to this result:

f0d400dd8daaffeaa31a369c41bb6b7982b15ad47a8c07000000000000000000

And now you hopefully remember that we were running everything in Little Endian. To finalize the process we need to convert it back to Big Endian and finally get to this hexadecimal number:

SELECT TO_HEX(REVERSE(SHA256(SHA256(b_header))));

And that’s the result:

000000000000000000078c7ad45ab182796bbb419c361aa3eaffaa8ddd00d4f0

that you now may compare to the actual header hash the next block refers to:

Prepare the inner loop

We’re going to wrap everything into a while-loop, add a break-out condition for safety reasons and start with a comparison of the just found hash and a target. Because that’s what it’s all about: Find a “number” (hash) that is lower than another “number” (target).

The target value is hidden in the bits field. And as already mentioned, we need to do the math to get the numeric target. The mantissa comes from the last 3 bytes, the exponent is the first byte. And the target comes from this equation:

target = mantissa * 256 ^ exponent

And this, well, leads to a pretty big number. Actually to big to fit into an INT64. We have to store it into a FLOAT64 and to make it comparable against the previously calculated hash, we need to cast the hash to FLOAT64, too.

Here’s the loop containing the condition, that returns the nonce — that we are looking for and a little break-out-statement, because we’re just testing how it’s working:

# skipping previous declarations from above# [...]DECLARE mantissa INT64DECLARE exponent INT64DECLARE target FLOAT64;DECLARE max_iterations INT64 DEFAULT 100;DECLARE iteration INT64 DEFAULT 0;SET exponent = CAST(CONCAT("0x", SUBSTRING(bits, 0, 2)) AS INT64)SET mantissa = CAST(CONCAT("0x", SUBSTRING(bits, 2, 4)) AS INT64);SET target = mantissa * POWER(256, exponent);WHILE true DO    SET header         TO_HEX(REVERSE(FROM_HEX(version))) ||        TO_HEX(REVERSE(FROM_HEX(hash_prev_block))) ||        TO_HEX(REVERSE(FROM_HEX(merkle_root))) ||        TO_HEX(REVERSE(FROM_HEX(header_datetime))) ||        TO_HEX(REVERSE(FROM_HEX(bits))) ||        TO_HEX(REVERSE(FROM_HEX(nonce)));    SET b_header = FROM_HEX(header);    SET header_hash = TO_HEX(REVERSE(SHA256(SHA256(b_header))));    IF CAST(CONCAT("0x", header_hash) AS FLOAT64) < target THEN        SELECT nonce;        BREAK;    END IF;    IF iteration > max_iterations THEN        SELECT "No nonce found";        BREAK;    END IF;    SET iteration = iteration + 1;END WHILE;

Complete the loop

Yeah well — isn’t that something? The only thing we need to do now is to actually iterate through the nonce to let the query find the correct value. To have an iterable variable we need one of the type FLOAT64. I will set the value a little bit under the expected target, to speed up the testing:

DECLARE nonce_dec FLOAT64 DEFAULT 3371190464; 

Now, after the loop starts and before we collect all header details,we need to get the hexadecimal nonce. And at the end of the loop, we increment the decimal nonce:

WHILE true DO    SET nonce = FORMAT("%X", nonce_dec);    SET header =        [....]    SET nonce_dec = nonce_dec + 1;END WHILE;

Adding the second loop

Now as we already learned, it may not be enough to test 2⁶⁴ possible numbers to find a fitting nonce. That’s why we’re going to add another loop to use the version field for some additional search space. Unfortunately this is a little more complicated. So, what do we need? Binary numbers!

This is the version for our famous block # 727155. Again we’re using this as an example. If you’d like to mine a new block, you need to adjust at least the soft fork part.

0x20002000

In binary that is:

00110100010011011100000000000100

The last 13 bits are representing the soft work readiness. That’s a given value. The version is pre-defined to be (at least) 001 for the first 3 bits. We’re taking the easy route here and are going to declare this in binary already. The remaining 16 bits are up and ready to be iterated through:

DECLARE soft_forks STRING DEFAULT "0000000000000";DECLARE version_roller INT64 DEFAULT 1;DECLARE version_roller_bin STRING;DECLARE version_bits STRING DEFAULT "001";

Please note, that I’m setting the version_roller to 1— that’s the one used in the block we are working on. Again, this is to speed up the demonstration here.

We will use an additional outer loop to iterate over the version roller. The iteration comes at the end, at the beginning of the loop we need to process the decimal value to get 16 bits out from it and press it into the hexadecimal format:

main_loop: WHILE true DO        SET version_roller_bin = SUBSTR(bqutil.fn.to_binary(version_roller), -16);    SET version = FORMAT("%X", bqutil.fn.from_binary(CONCAT(version_bits, version_roller_bin, soft_forks)));WHILE true DO        [....]    END WHILE;    SET version_roller = version_roller + 1;END WHILE;

Take care of the label I set here to address the loop: MAIN_LOOP. I have to reference the outer loop when breaking from inside the inner loop:

    [...]    BREAK main_loop;    [...]

Check out the full script in final part.

Congratulations and Conclusion

Basically that’s it. That’s how the full script should look like this (gist.github.com). Feel free to increase the value for max_iterations and set the starting value for nonce_dec to 0 and see how long it will take Google to find the correct nonce.

This is a lot of weird SQL stuff and far away from SELECT * FROM table. Is it worth it? Well, I set the starting nonce to 3370194460 and executed the script.

Spoiler Alert: After 10 minutes I stopped the query. Another approach (see below) seems way faster, though it’s a cheating with the actual calculations.

Disclaimer

I will not loose much words about Proof of Work. The process itself is sophisticated and somehow thoughtfull… as well as a little weird. But above all it’s also a huge wast of energy and there are better ways to achieve the same outcome. I’d like to end with a quote from another author on Medium who said:

You’ve got to wonder what we’d achieve if we used even a fraction of this computing power for medical research instead…

Additional ressources

This is a pretty good and helpful medium article about the Blockchain header by RJ Rybarczyk. This is a website that provides a lot of technical background information as well as tools to calculate hashes or browse the Blockchain.

A couple of years ago Uri Shaked also wrote about this topic. I stumbled over his article while doing research. But he was pursuing a different approach. First of all he was using a random feature to find a fitting nonce. I also considered this before, but as you cannot ensure to ge the same random value twice, you will waste a lot of time (he actually calculated the same nonce within 20 seconds, which still is faster than my approach). Besides that he was using sub-queries to create temporary tables filled with the nonce.